When it comes to electronics, there are three basic components resistors, capacitors and Inductors. We have already talked about them and gone through the basic working principles behind them. As we know capacitors are fundamental components in electronics, essential for storing and releasing energy. You can find them used in various use cases from decoupling to filters or even as backup power with the new supercapacitors. One key aspect of their operation is capacitor charge time, which is a critical factor in many applications. In this article, we will look into the capacitor charge time and how to calculate it.

Capacitor Charge Time - Basics

As we know a capacitor when connected to a power supply with take some time to charge. Since all the circuits have some kind of resistance in them, whether it's the resistance of the connecting wires or the internal resistance of the power source such as batteries we can always consider that a resistor is present in series with a capacitor. The below image shows a simple RC circuit where the resistor R can be an considered as an actual resistor or the resistance from wires and power source. Now the charge time for our capacitor C depends on the value of the resistor R. 

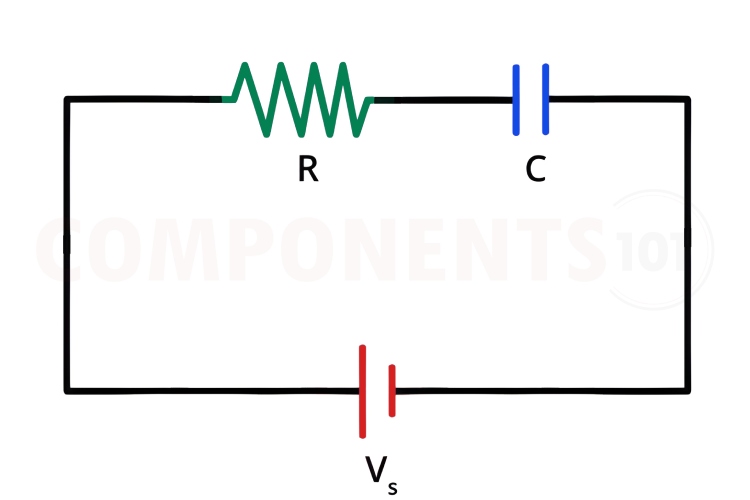
So, the charge time of a capacitor is primarily determined by the capacitor charge time constant denoted as ? (pronounced tau), which is the product of the resistance (R) in the circuit and the capacitance (C) of the capacitor. Capacitor charging time can be defined as the time taken to charge the capacitor, through the resistor, from an initial charge level of zero voltage to 63.2% of the DC voltage applied or to discharge the capacitor through the same resistor to approximately 36.8% of its final charge voltage.  The capacitor charge time formula can be expressed as:

?=RC

Where:

? (tau) is the time constant in Seconds. R is the resistance in ohms (Ω). C is the capacitance in farads (F).

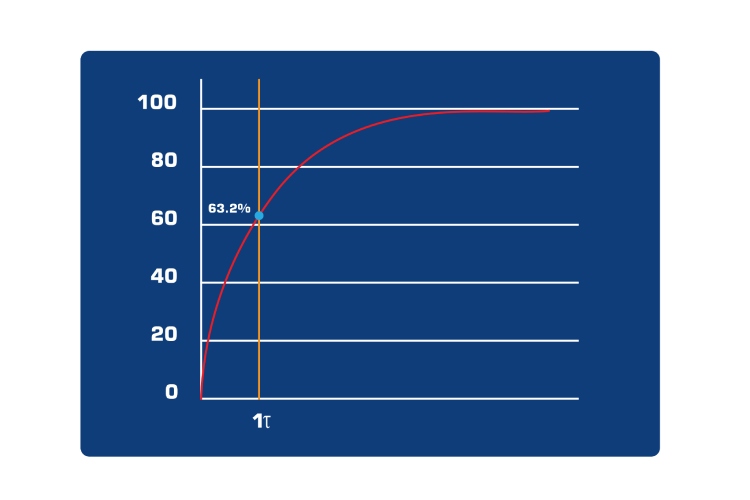
The below is an image of capacitor charge time graph, on the Y-axis we have the voltage and on X-axis we have our time constant ? (tau). As discussed earlier the time taken for the capacitor to charge to 63.2% is 1? as indicated in the graph below.

Here is a simple simulation showing the charging of the capacitor. For simplicity of the calculation, we have added a series resistor of our own to it. You can also check out our online capacitor charging time calculator if you want to make some quick calculations. 

As you can see in the voltage-time plot, at first the voltage increases rapidly, and then it slows down until it reaches the full voltage. As we know one time constant is the time taken for the capacitor to charge up to 63.2% of the full voltage. So we have marked the x-axis with the time constant. From the resulting plot, you can see that with 5? the capacitor charges up to 99.3% of the full voltage. With that considering that the capacitor is fully charged at 5? we can calculate the capacitor using this capacitor charge time equation:

T = 5? = 5RC

For example, in the above simulation, we have used a 100µF capacitor and a 10kΩ resistor. So the time taken to charge the capacitor can be calculated as follows:

T=5RC = 50.000110000=5s

I.e, the capacitor will be fully charged within 5 seconds.

Frequently Asked Questions About Capacitor Charge Time

What is a faster way to charge a capacitor?

As we know the charging time of a capacitor is five times the time constant, and it is dependent on the capacitance and the series resistance. Since we cannot change the capacitance, the next best thing is to minimize the series resistance.

How long does it take for a capacitor to fully charge?

A capacitor never gets charged to 100%. But you can calculate the time taken to charge the capacitor using the capacitor time constant which is calculated by multiplying R and C (tau = R * C). It takes about 5 times the time constant for a capacitor to reach 99% charged. The higher the resistance or capacitance, the longer it takes to charge

If a capacitor is connected to a battery directly, it should be charged instantaneously since there is no resistor in between them, since the time constant will be zero as per the above-given formula. But that's not the case. Why?

In an ideal scenario, the value of resistance will be zero and the capacitor should be charged instantaneously. But in real life, the value of resistance will never be zero, there will be factors we need to consider such as the resistance of the connecting wire, the internal resistance of the power source etc.

Why consider 5? as the full charge level when it was only 99.3%?

As you can see on the plot at 5? the rate of increase of voltage is very negligible and continues to decrease, it would take infinite time to charge the battery to a 100% level.

Can a capacitor be charged 100%?

In practice charging a capacitor to 100% will take infinite time.