Chebyshev filters are analog or digital filters that are used to separate one band of frequencies from another. Even though they cannot match the performance of windowed-sink filters, they have steeper roll-off than Butterworth filters and are more than suitable for many applications. There are two types of Chebyshev filters type I with passband ripple and type II with stopband ripple. Type I Chebyshev filters are usually referred to as "Chebyshev filters", while type II filters are usually called "inverse Chebyshev filters". Chebyshev filters have a built-in passband ripple, therefore for some applications, filters with a smoother response in the passband but a more erratic response in the stopband are preferable.

Features Of Chebyshev Filter

Some of the key features of Chebyshev filter are the following.

• Roll Off: One of the main aspects of Chebyshev filters is that its steep roll-off. Chebyshev filters reaches the maximum roll-off faster than any other type of filter. Because of this, Chebyshev filters are widely used in many RF applications where steep transition between passband and stop-band is required and is used to remove unwanted intermodulation of harmonics and such.
• Ripple: as mentioned earlier Chebyshev filters offers steep roll-off, but it comes with the cost of ripple. So, it is important to keep this in mind while using the Chebyshev filters.
• Cut-off frequency: In light of the in-band ripple, the conventional definition of the cut-off frequency at the point at which the response drops to -3 dB does not apply to Chebyshev filters. Instead, the cut-off is defined as the point at which the gain finally reaches the value of the ripple.

Types of Chebyshev Filters

Chebyshev filters are classified into two types, namely type-I Chebyshev filter and type-II Chebyshev filter.

Type-I Chebyshev Filters

This is the basic type of Chebyshev filter. The gain response, G_n as a function of the angular frequency, ω for an n-th order Chebychev filter can be expressed in the form of the function below:

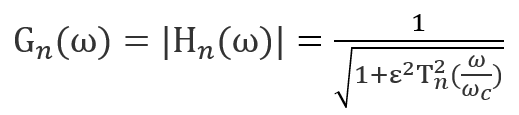
Where:

    ε = ripple factor

    ω_c is the cut-off frequency

    T_n is the Chebychev polynominal of the nth order.

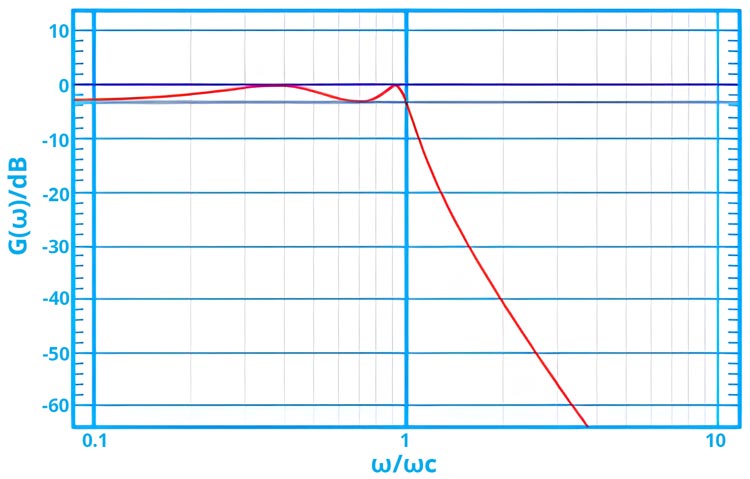
Frequency response of a fourth-order type I Chebyshev low-pass filter with ε = 1.

Equiripple performance is visible in the passband. In this band, the filter interchanges between -1 & 1 so the gain of the filter interchanges between max at G = 1 and min at G =1/√(1+ε²). At the cutoff frequency, the gain is equal to G =1/√(1+ε²) and as the frequency rises, it continues to fail into the stop band. Below is a demonstration of the filter's behaviour.

Here is a example MATLAB script to simulate type I Chebyshev low-pass filter:

% Filter specifications
Rp = 1;          % Passband ripple in dB
Rs = 40;         % Stopband attenuation in dB
Wp = 0.4;        % Passband edge frequency
Ws = 0.6;        % Stopband edge frequency
% Design the Chebyshev Type I filter
[N, Wn] = cheb1ord(Wp, Ws, Rp, Rs);   % Calculate the order N and cutoff frequency Wn
[b, a] = cheby1(N, Rp, Wn);           % Design the filter
% Analyze the filter
freqz(b, a, 1024);                    % Plot the magnitude and phase response
title('Chebyshev Type I Low-pass Filter');

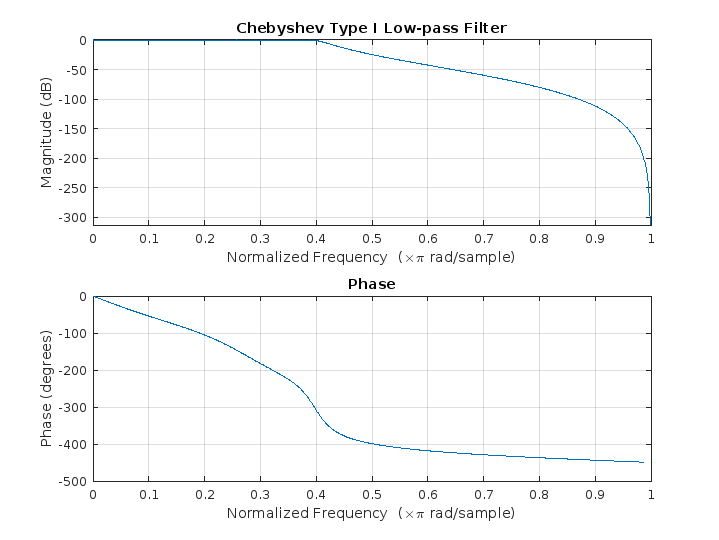
And here is the simulation result.

Type-II Chebyshev Filter

The type II Chebyshev filter is also known as an inverse Chebyshev filter. The inverse Chebyshev filter are less common because it does not roll off as fast as the Type I and requires more components built. Even though it does not have ripple in the passband, it does have equiripple in the stopband. The gain of the Type II Chebyshev filter is expressed as follows:

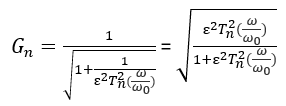
In the stopband, the Chebyshev polynomial oscillates between -1 and 1. The smallest frequency at which this maximum is attained is the cutoff frequency ω₀.

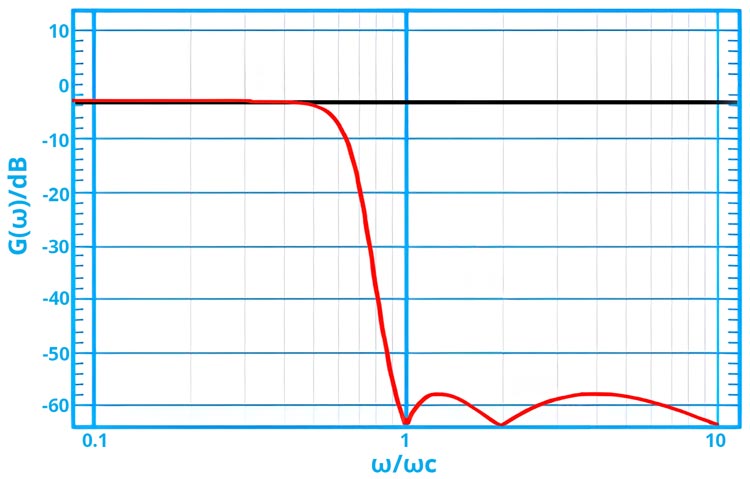
The frequency response of a fifth-order type II Chebyshev low-pass filter with ε = 0.01

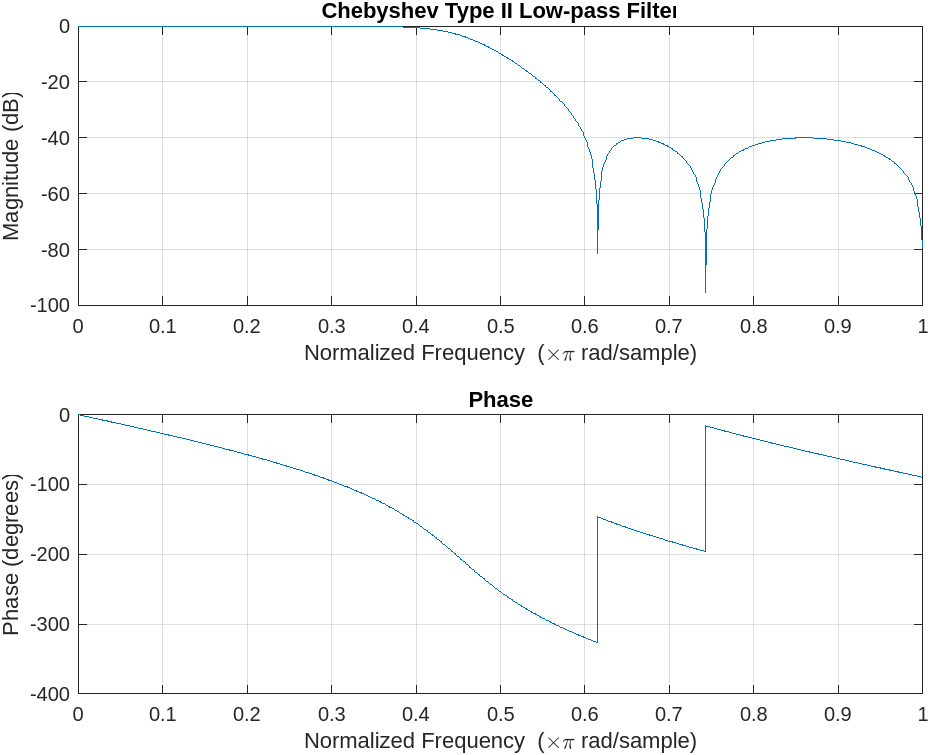
Here is the MATLAB script to simulate type II Chebyshev low-pass filter.

% Filter specifications
Rp = 1;          % Passband ripple in dB (usually very small or zero for Type II)
Rs = 40;         % Stopband attenuation in dB
Wp = 0.4;        % Passband edge frequency
Ws = 0.6;        % Stopband edge frequency
% Design the Chebyshev Type II filter
[N, Wn] = cheb2ord(Wp, Ws, Rp, Rs);   % Determine order and cutoff frequency
[b, a] = cheby2(N, Rs, Wn);           % Compute filter coefficients
% Analyze the filter response
freqz(b, a, 1024);                    % Visualize magnitude and phase response
title('Chebyshev Type II Low-pass Filter');

And here is the simulation result.

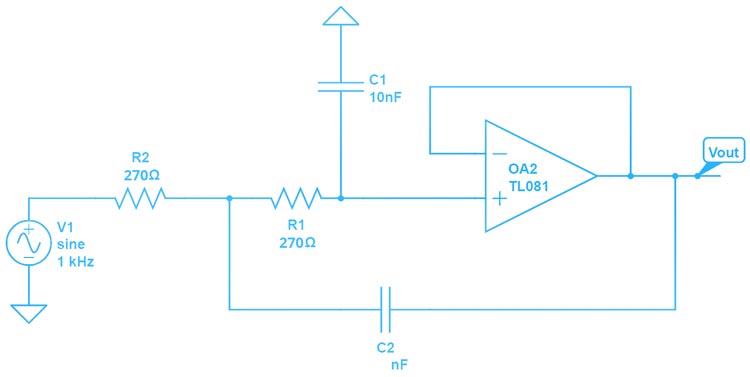
Example Chebyshev Filter Circuits

The image below shows the circuit of a 2nd-order Chebyshev Type I Low-Pass filter based on the Sallen-Key topology.

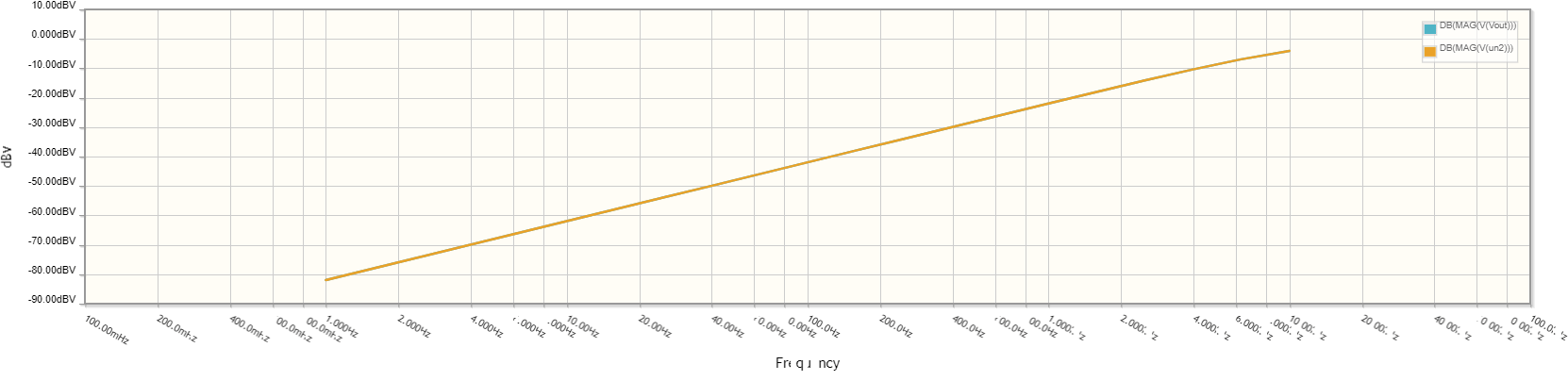
Here is the frequency domain plot for the same circuit.

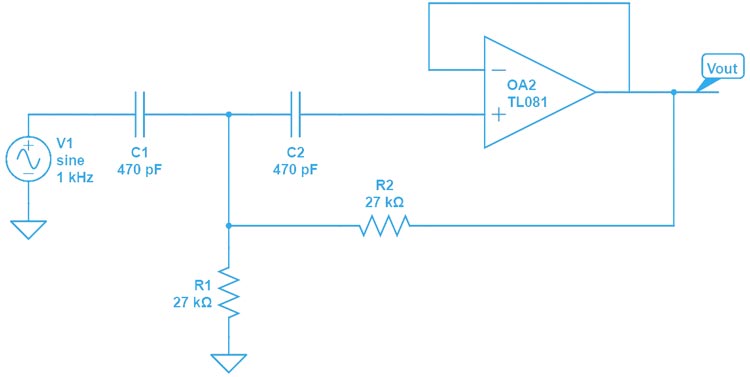
The image below shows the circuit of a 2nd-order Chebyshev Type I High-Pass filter based on the Sallen-Key topology.

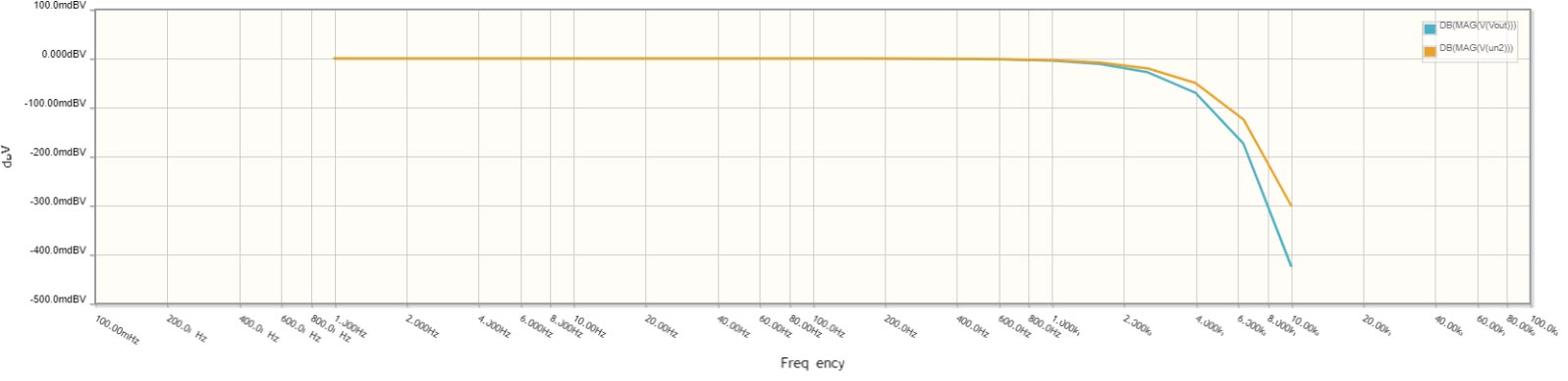
Here is the frequency domain plot for the same circuit.